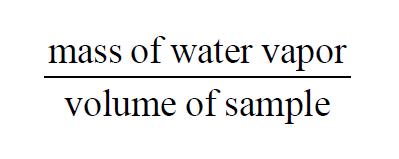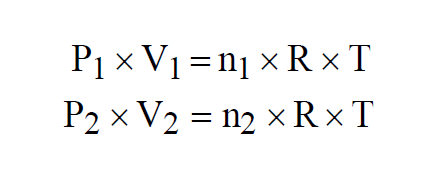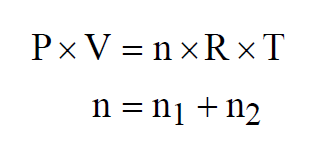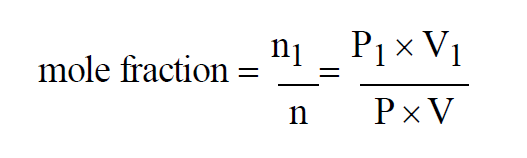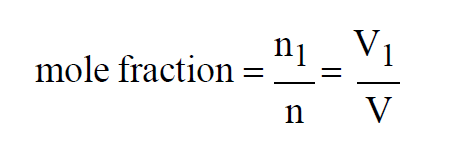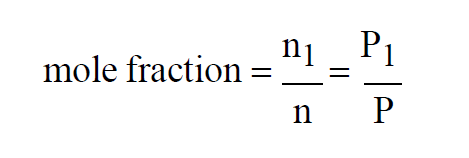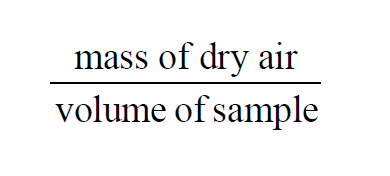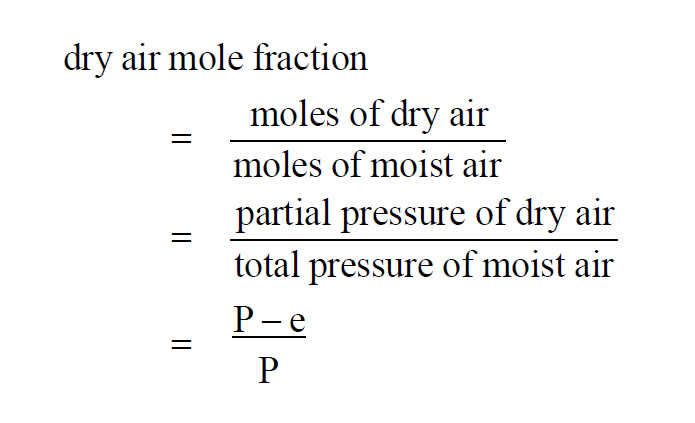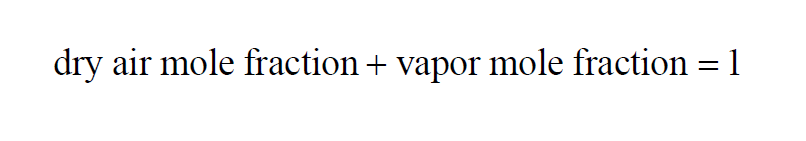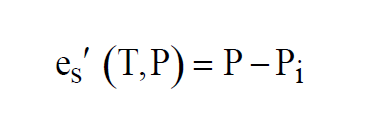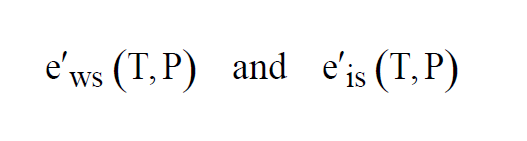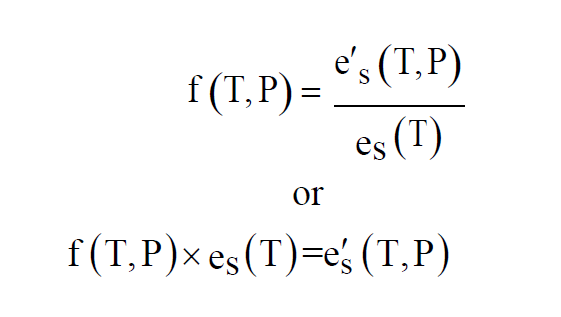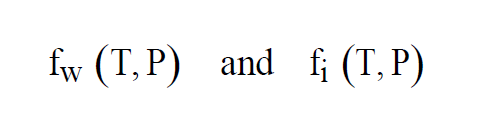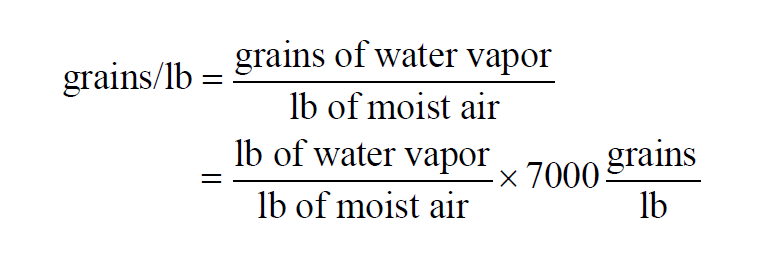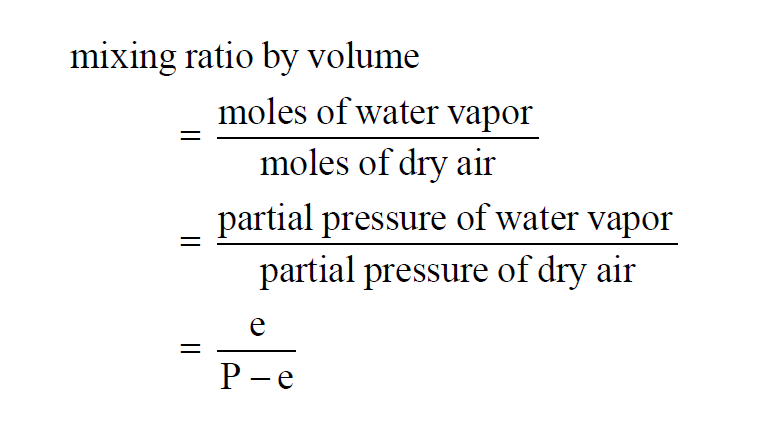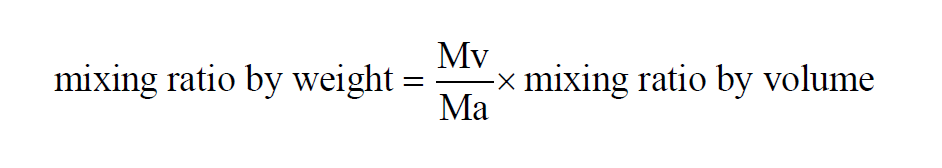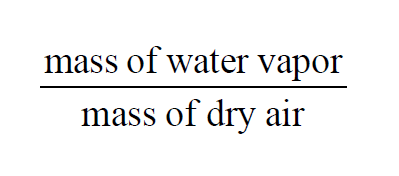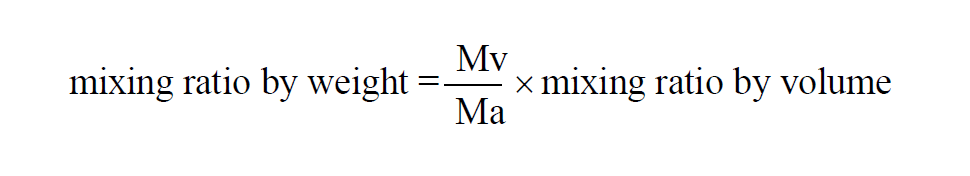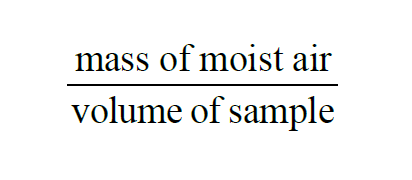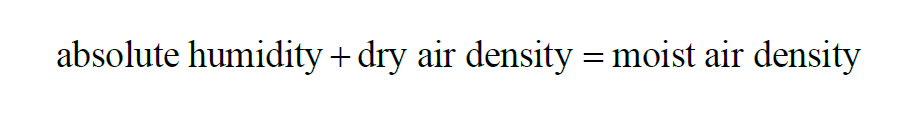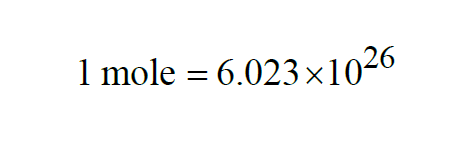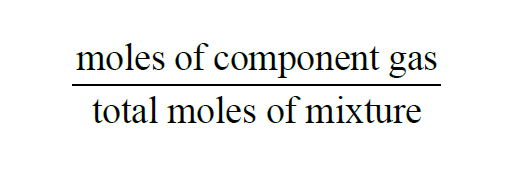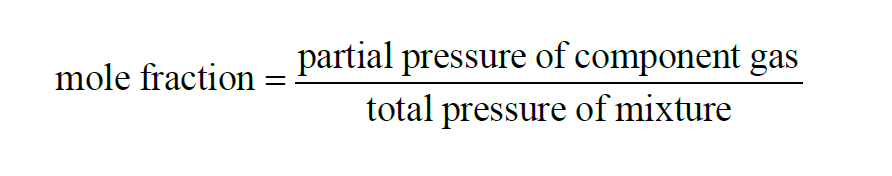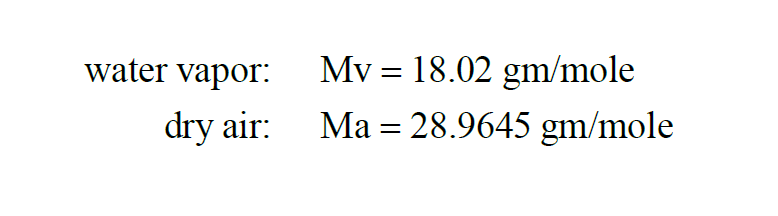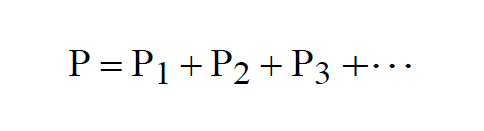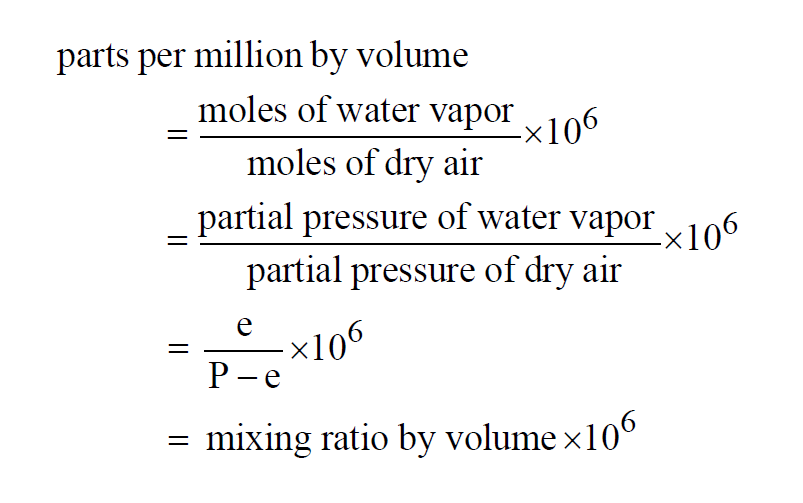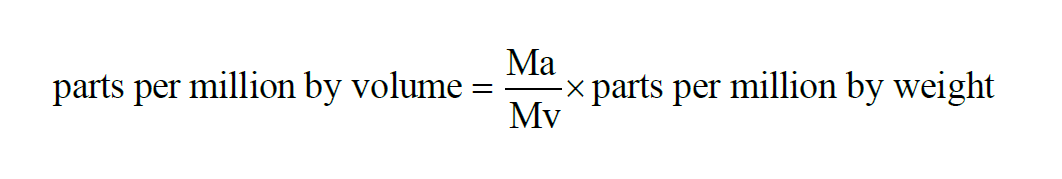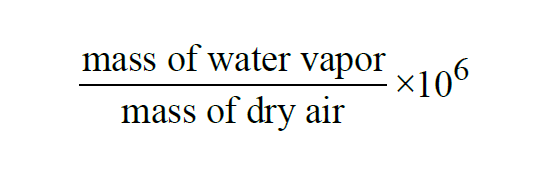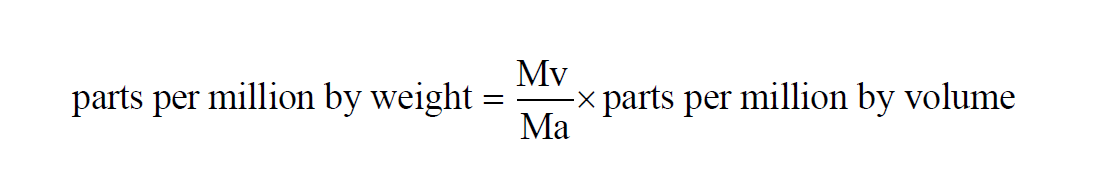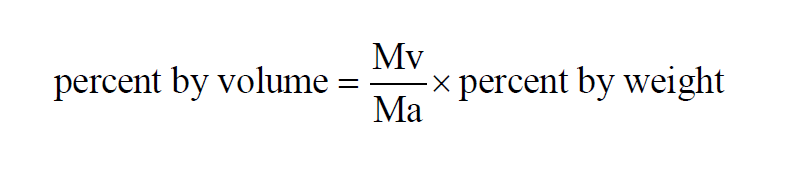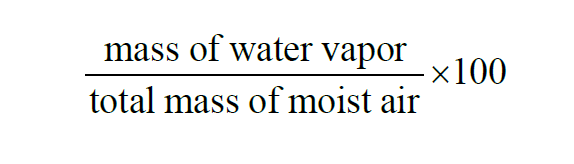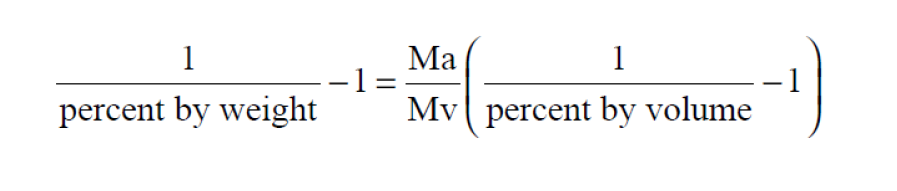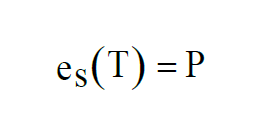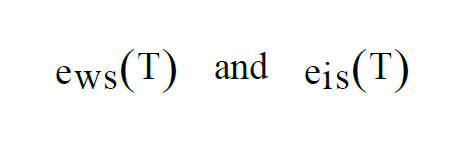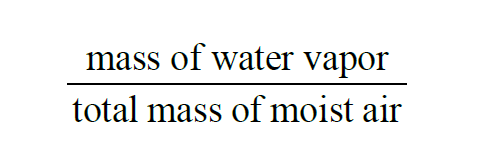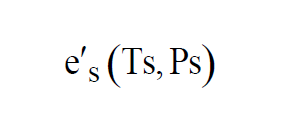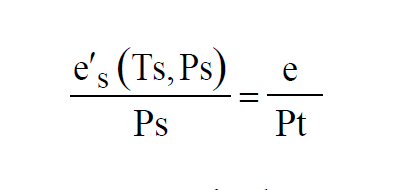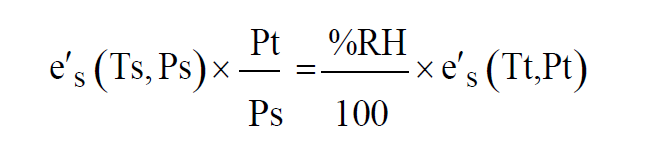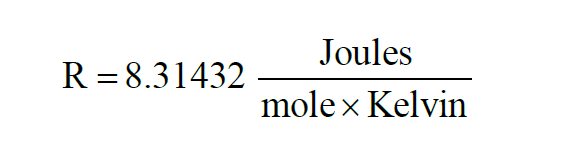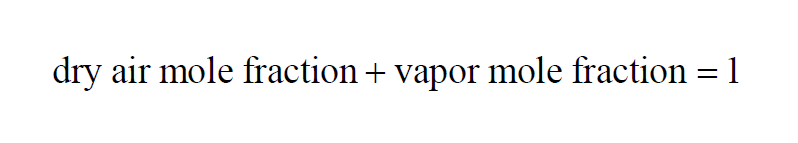Basic Humidity Definitions
Absolute Humidity, Vapor Concentration, Water Vapor Density
From Wexler(1), Absolute Humidity, Vapor Concentration, and Water Vapor Density are all the same. In a moist air sample, they all equal
Using the Ideal Gas Law, the Molecular Weight of water vapor, and Partial Pressures,
Dalton's Law states that the Ideal Gas Law applies to mixtures of ideal gases. Two ideal gases, n1 moles of the first gas and n2 moles of the second, both at the same temperature, must each individually satisfy the Ideal Gas Law.
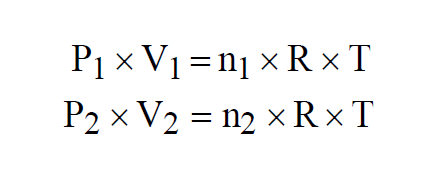
If the two gases are combined to form a mixture of n moles, again at the same temperature, then
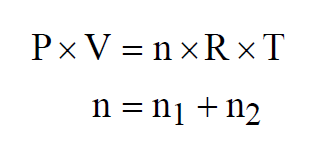
Since temperatures are all the same, the Mole Fraction of the first gas in the mixture must satisfy
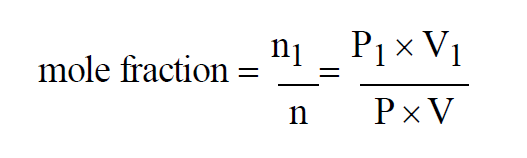
If, in addition to the temperatures, all three pressures are the same, then
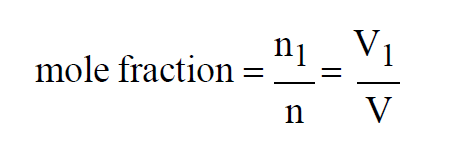
If, in addition to the temperatures, all three volumes are the same, then
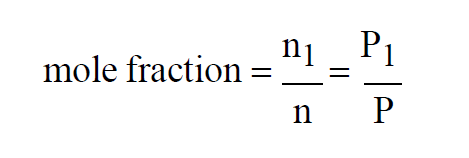
Similarly for the Mole Fraction of the second gas. Dalton's Law also applies to mixtures of more than two gases.
The Dew Point of a moist air sample is the temperature to which the sample must be cooled to reach saturation with respect to liquid water. Using the Enhanced Saturation Vapor Pressure function,

The Enhanced Saturation Vapor Pressure at the Dew Point temperature and pressure P is the same as the Partial Pressure of the water vapor in the moist air sample at the current temperature T and the same pressure P.
In a given sample of moist air, the Dry Air Density is
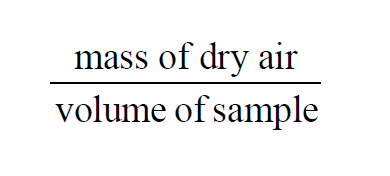
Using the Ideal Gas Law, the Molecular Weight of dry air, and Partial Pressures,
The Dry Air Mole Fraction Wexler(1) in a moist air sample is
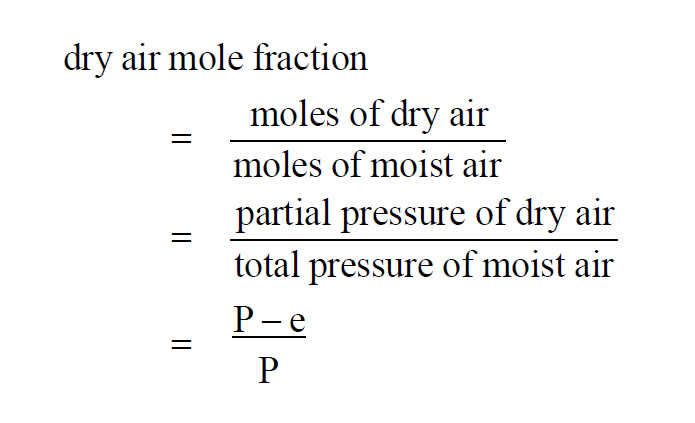
Here P is the pressure of the moist air sample and e is the Partial Pressure of the water vapor present in the sample. The Dry Air Mole Fraction of a moist air sample does not change when either temperature or pressure changes. Dry Air Mole Fraction and Vapor Mole Fraction are related by
Enhanced Saturation Vapor Pressure
Enhanced Saturation Vapor Pressure, or Saturation Vapor Pressure of Moist Air, is a function of both pressure and temperature. Like Saturation Vapor Pressure, it can best be described by a lab setup. Imagine a chamber whose temperature T and pressure can be controlled. The chamber is partially filled with water. The pressure of the space over the water can be measured. Initially, the remaining space is filled with dry air at initial pressure Pi. At a fixed temperature, water molecules will leave the water and enter the dry air above at a fixed rate.
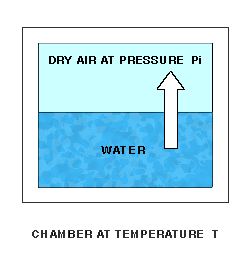
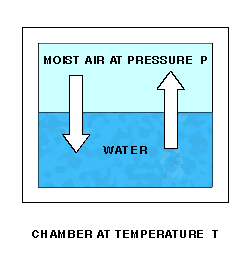
As water molecules accumulate over the liquid water, the pressure there will increase, and molecules will re-enter the liquid at an increasing rate. Finally, water molecules will be entering and leaving the liquid at the same rate, giving equilibrium and a constant final pressure P over the water.
The Enhanced Saturation Vapor Pressure (Saturation Vapor Pressure of Moist Air) at temperature T and pressure P is the Partial Pressure due to the water vapor in the moist air.
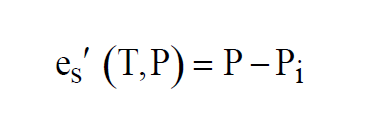
At temperatures above freezing, equilibrium is achieved over water. At temperatures below freezing, equilibrium can be achieved either over water or over ice. This gives two functions, as with Saturation Vapor Pressure,
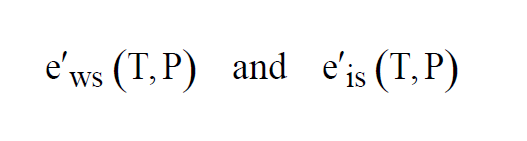
The two functions agree for values of T above freezing. They differ for values of T below freezing.
The Enhancement Factor at temperature T and pressure P is the ratio of the Enhanced Saturation Vapor Pressure to the Saturation Vapor Pressure. One source of approximating formulas is Greenspan(3).
As with Enhanced Saturation Vapor Pressure and Saturation Vapor Pressure, there are really two functions, one for equilibrium over water, the other for equilibrium over ice.
The Frost Point of a moist air sample is the temperature to which the sample must be cooled to reach saturation with respect to ice. Using the Enhanced Saturation Vapor Pressure function,

The Enhanced Saturation Vapor Pressure at the Frost Point temperature and pressure P is the same as the Partial Pressure of the water vapor in the moist air sample at the current temperature T and the same pressure P.
In a given sample of moist air, the Grains per Pound is
The Grains per Pound of a moist air sample does not change when either temperature or pressure changes. With the usual identification of weight and mass,
The Ideal Gas Law relates the pressure, volume, moles, and temperature of a sample of ideal gas.

The Mixing Ratio by Volume of a moist air sample is really the Mixing Ratio by Moles.
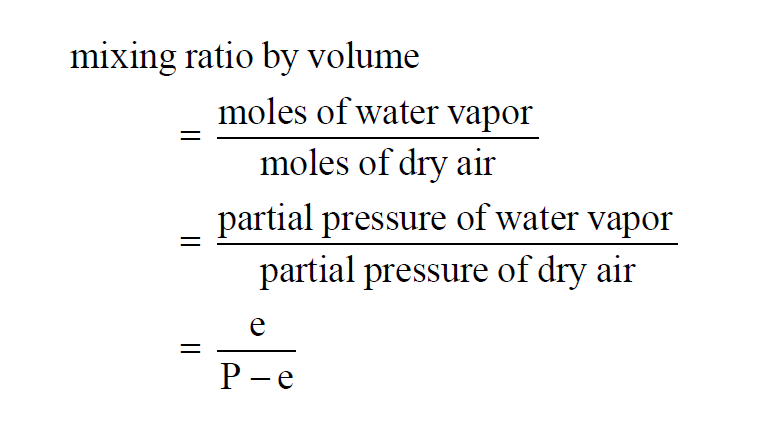
Here P is the pressure of the moist air sample and e is the Partial Pressure of the water vapor present in the sample. The Mixing Ratio by Volume of a moist air sample does not change when either temperature or pressure changes. The Mixing Ratio by Volume is related to the Mixing Ratio by Weight through the Molecular Weights of water vapor and dry air.
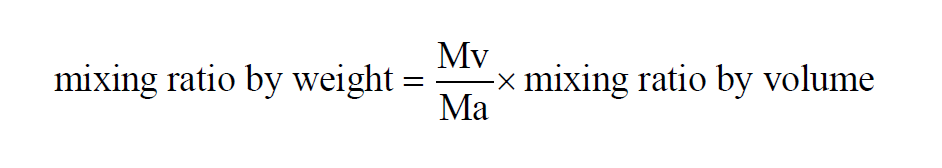
From Wexler(1), in a given sample of moist air, the Mixing Ratio by Weight is
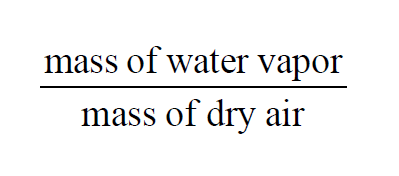
The Mixing Ratio by Weight of a moist air sample does not change when either temperature or pressure changes. The Mixing Ratio by Weight is related to the Mixing Ratio by Volume through the Molecular Weights of water vapor and dry air.
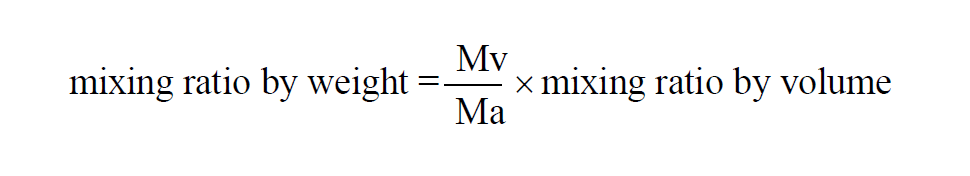
In a given sample of moist air, the Moist Air Density is
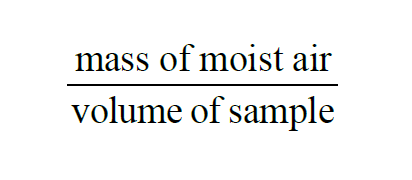
Moist Air Density is the sum of Dry Air Density and Absolute Humidity.
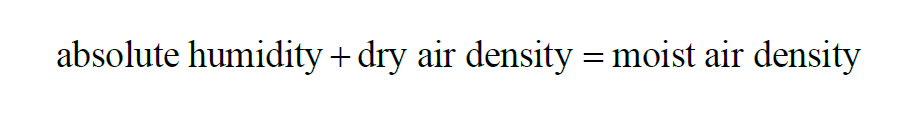
A Mole is like a dozen or a gross, only much larger. From Wexler(1),
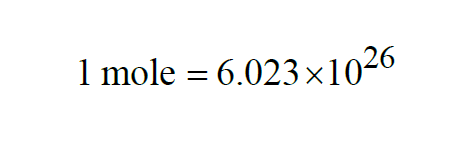
From Wexler(1), the Mole Fraction of a component gas present in a mixture of gases is
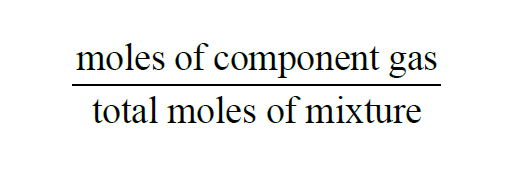
From Dalton's Law,
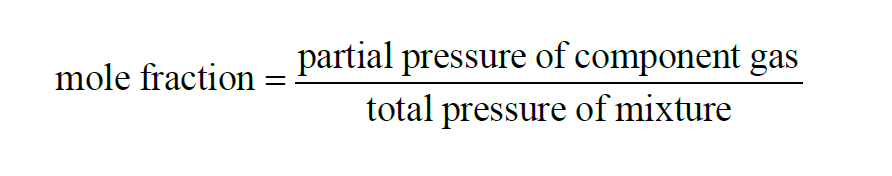
The Molecular Weight of a substance is the weight in grams of a mole of that substance. From Wexler(1),
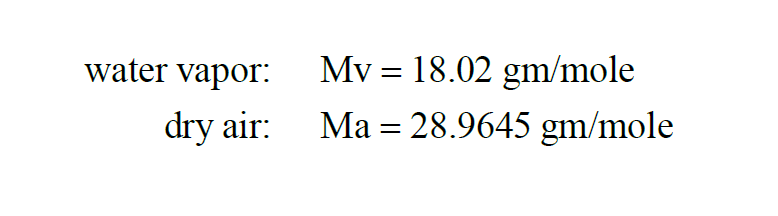
The pressure P of a mixture of gases is the sum of the Partial Pressures of the component gases.
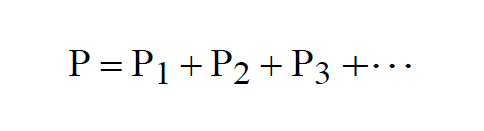
Where Pi, the Partial Pressure of the ith component gas, is the pressure that would be measured if the volume were occupied by only the ith component gas. This is a consequence Dalton's Law.
In a sample of moist air, the total pressure is denoted P, and the Partial Pressure of the water vapor present is denoted e. Then the Partial Pressure of the dry air in the sample must be (P-e).
Parts Per Million by Volume
Parts Per Million by Volume is really Parts Per Million by Moles. It is the Mixing Ratio by Volume expressed in parts per million. In a moist air sample,
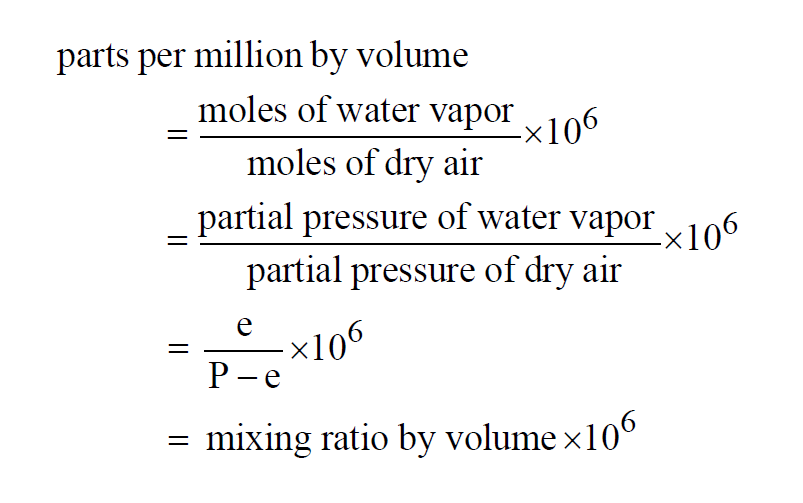
Here P is the pressure of the moist air sample and e is the Partial Pressure of the water vapor present in the sample. The Parts Per Million by Volume of a moist air sample does not change when either temperature or pressure changes. The Parts per Million by Volume is related to the Parts per Million by Weight through the Molecular Weights of water vapor and dry air.
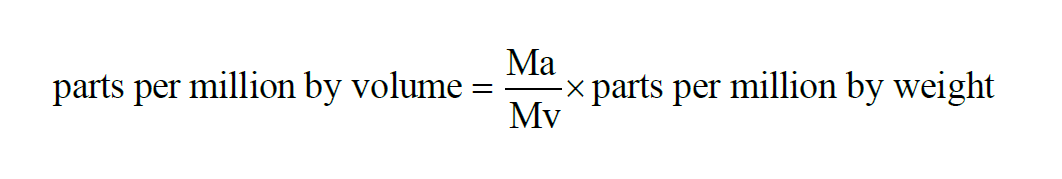
Parts Per Million by Weight
The Parts per Million by Weight of a given sample of moist air is the Mixing Ratio by Weight expressed in parts per million,
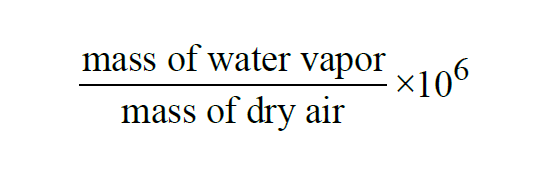
The Parts per Million by Weight of a moist air sample does not change when either temperature or pressure changes. The Parts per Million by Weight is related to the Parts per Million by Volume through the Molecular Weights of water vapor and dry air.
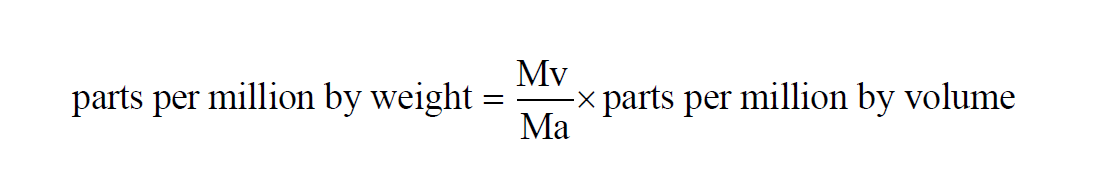
Percent by Volume Wexler(1) is really Percent by Moles. It is the Vapor Mole Fraction expressed as a percent. In a moist air sample,

Here P is the pressure of the moist air sample and e is the Partial Pressure of the water vapor present in the sample. The Percent by Volume of a moist air sample does not change when either temperature or pressure changes. The Percent by Volume is related to the Percent by Weight through the Molecular Weights of water vapor and dry air.
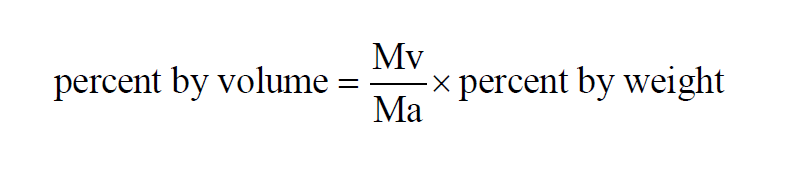
From Wexler(1), the Percent by Weight of a given sample of moist air is the Specific Humidity expressed as a percent,
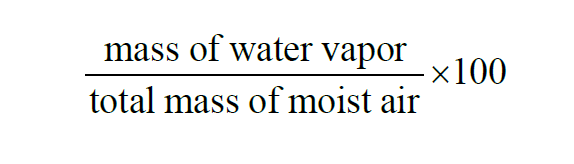
The Percent by Weight of a moist air sample does not change when either temperature or pressure changes. The Percent by Weight is related to the Percent by Volume through the Molecular Weights of water vapor and dry air.
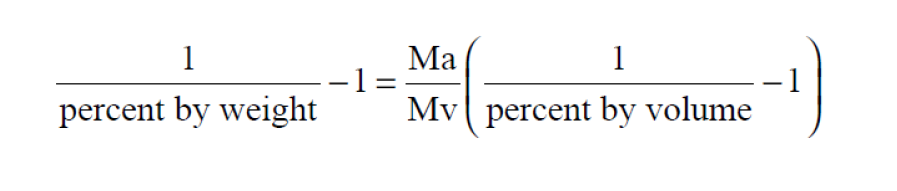
Relative Humidity is the ratio of the amount of water vapor in a sample to the maximum amount possible at the same temperature and pressure. It is expressed as a percent. In a sample of moist air at pressure P and temperature T, using the Enhanced Saturation Vapor Pressure,

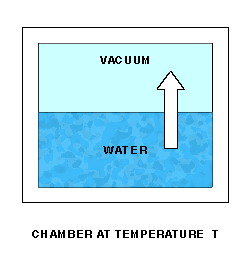
Saturation Vapor Pressure
Saturation Vapor Pressure is a function of temperature. Sonntag(2) is one source of approximating formulas. The function can best be described by a lab setup. Imagine a chamber whose temperature T can be controlled. The chamber is partially filled with water. Initially, the remaining space is a vacuum. The pressure P of the space over the water can be measured. At a fixed temperature, water molecules will leave the water and enter the space above at a fixed rate.
As water molecules accumulate over the liquid water, the pressure there will increase, and molecules will re-enter the liquid at an increasing rate. Finally, water molecules will be entering and leaving the liquid at the same rate, giving equilibrium and a constant pressure P over the water.
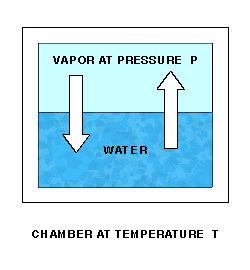
The equilibrium pressure P is the Saturation Vapor Pressure at temperature T.
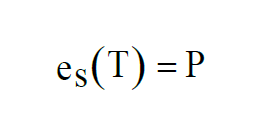
At temperatures above freezing, equilibrium is achieved over water. At temperatures below freezing, equilibrium can be achieved either over water or over ice. This gives two functions,
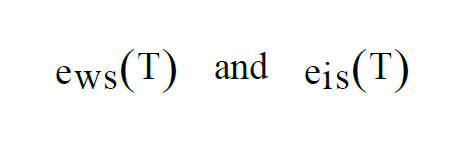
The two functions agree for values of T above freezing. They differ for values of T below freezing.
From Wexler(1), in a given sample of moist air, the Specific Humidity is
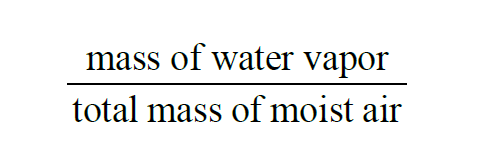
The Specific Humidity of a moist air sample does not change when either temperature or pressure changes. In terms of Partial Pressures and Molecular Weights,

Two-Pressure/Two-Temperature Humidity Generator
A Two-Pressure/Two-Temperature Humidity Generator has a chamber, the Test Chamber, in which the humidity can be set to a predetermined value.
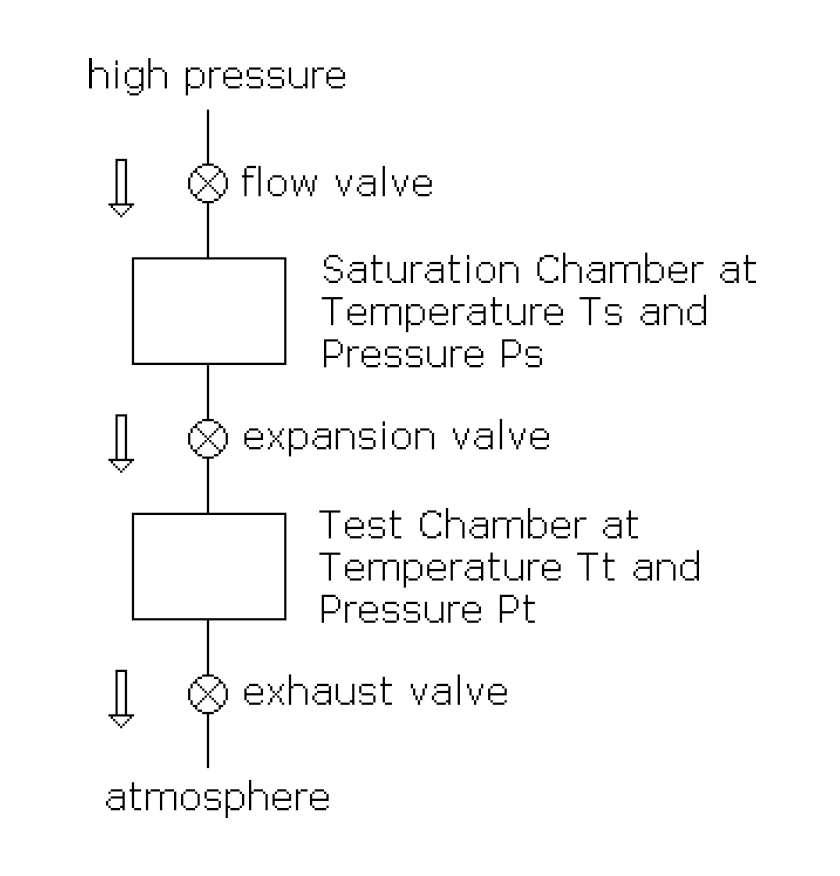
The pressures and temperatures in both chambers can be controlled. If the valve is not present at the Test Chamber exhaust, then Test Pressure is atmospheric pressure. If the apparatus is such that both temperatures are always the same, it is called a Two-Pressure Generator. If the apparatus is such that both pressures are always the same, it is called a Two-Temperature Generator. The air in the Saturation Chamber is saturated. That is, Partial Pressure of the water vapor in the Saturation Chamber is
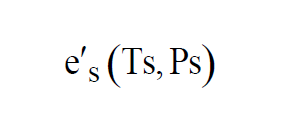
The same moist air flows through both chambers, so the Vapor Mole Fractions must be the same.
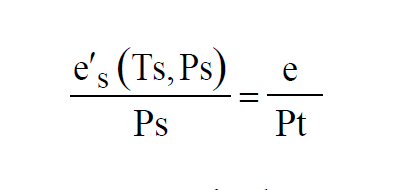
Where e is the Partial Pressure of the water vapor in the Test Chamber. If it is desired to achieve a specified Relative Humidity in the Test Chamber at a given test temperature and pressure, then the saturation temperature and pressure can be adjusted accordingly. Using the equation for Relative Humidity to get rid of the variable e gives
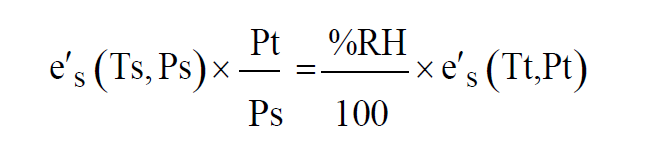
For a desired Relative Humidity, test temperature, and test pressure, suitable values of saturation pressure and temperature must be found to satisfy this equation.
The Universal Gas Constant is denoted R. From Wexler(1),
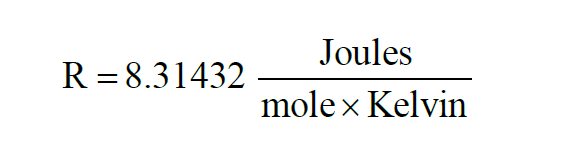
The Vapor Mole Fraction Wexler(1) in a moist air sample is

Here P is the pressure of the moist air sample and e is the Partial Pressure of the water vapor present in the sample. The Vapor Mole Fraction of a moist air sample does not change when either temperature or pressure changes. Vapor Mole Fraction and Dry Air Mole Fraction are related by
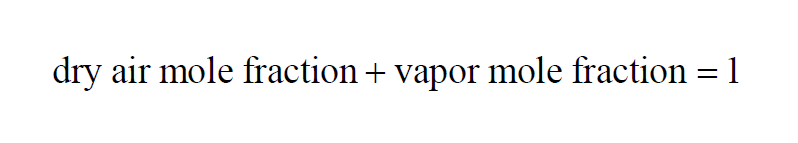
American Meteorological Society(5) (Also called aqueous vapor, moisture.) Water substance in vapor form; one of the most important of all constituents of the atmosphere.
Its amount varies widely in space and time due to the great variety of both "sources" of evaporation and "sinks" of condensation that provide active motivation to the hydrologic cycle. Approximately half of all of the atmospheric water vapor is found below 2-km altitude, and only a minute fraction of the total occurs above the tropopause. Water vapor is important not only as the raw material for cloud and rain and snow, but also as a vehicle for the transport of energy (latent heat) and as a regulator of planetary temperatures through absorption and emission of radiation, most significantly in the thermal infrared (the greenhouse effect). The amount of water vapor present in a given air sample may be measured in a number of different ways, involving such concepts as absolute humidity, mixing ratio, dewpoint, relative humidity, specific humidity, and vapor pressure.
1Wexler, A. Humidity and Moisture, vol. 3, Reinhold Publishing, 1965
2Sonntag, D. "Important New Values of the Physical Constants of 1986, Vapour Pressure Formulations based on the ITS-90, and Psychrometer Formulae", Z. Meteorol., 1990, 40, pages 340-344.
3Greenspan, L. "Functional Equations for the Enhancement Factors for CO2-Free Moist Air", Journal of Research of the National Bureau of Standards - A. Physics and Chemistry, Vol. 80A, No. 1, January - February 1976; page 41, equation 3; page 42, equations 5 and 6, Table 1.4JOURNAL OF RESEARCH of the Notional Bureau of Standards-A. Physics and Chemistry
Vol. 81 A, No. 1, January-February 19775American Meteorological Society - https://glossary.ametsoc.org/wiki/Water_vapor
Page was last edited on 20 February 2012, at 16:27.